Mathematical sense, also known as number sense or numeracy, is a basic skill that lets people understand and use numbers with confidence and precision.
It goes beyond just being good at math; it includes an understanding of concepts, the ability to solve problems and a knowledge of what real mathematics is.
Why Mathematical sense is important
Developing a mathematical sense is essential for several reasons, spanning personal, educational, and professional domains. This is why:
Everyday Life Applications
Understanding mathematics assists in managing daily activities like making budgets, cooking meals, buying goods, and planning trips, among others. It helps individuals make informed decisions and handle practical situations efficiently.
Educational Success
A strong foundation in mathematics is essential for success at school especially at STEM (Science, Technology Engineering Mathematics) disciplines where many subjects require proficiency in mathematics which acts as the key determinant for further studies or career advancement.
Employment Opportunities
There are numerous occupations whereby people must be good in math, for example, engineering, computer science, economics, accountancy and finance, medicine and data analysis.
Possessing a healthy mathematical sense could result in you having a wider selection of jobs.
Competency in Technology
Mathematics is crucial to understand and use technology properly in a world that is increasingly becoming digital. This involves programming languages and data analysis as well as the understanding of algorithms and artificial intelligence.
Science Appreciation
Science’s language is mathematics. Understanding scientific principles through the grasp of these mathematical concepts are fundamental to participating in scientific researches and discoveries.
Financial Maturity
Some financial calculations such as interest rates, support repayments, investments and savings take assistance from maths.This knowledge is essential for personal finance management as well as economic stability.
Participatory Democracy
Understanding mathematics enables people to better comprehend what they watch or hear on media or see during election campaigns or policy debates which leads to more informed decisions by citizens based on reason than emotions
Cognitive Development
Working on math problems is an important factor of cognitive development, promoting intelligence, memory and attention. It also helps in promoting skills such as intellectual precision and being able to pay attention to details.
Cultural Appreciation
Mathematics is an integral part of human culture and history. Understanding mathematical successes can help to better understand how humans have developed as well as what has changed in terms of our mental heritage.
7 effective strategies
This complete guide covers seven most effective strategies that teachers and learners should consider when they want to develop mathematical sense effectively.
Building a Strong Foundation in Number Concepts
Comprehending number concepts well is the basis for understanding mathematics. Students must grasp fundamental points such as place value, number relationships (for instance addition and subtraction) and operations (multiplication and division).
This basic knowledge forms the platform on which more complex mathematical skills are built (source).
Key Practices for Building Number Concepts
| Illustrate abstract concepts using manipulatives and visual aids. |
| Counting routines and basic operational activities should be done daily. |
| Require students to give explanations for their numerical solutions. |
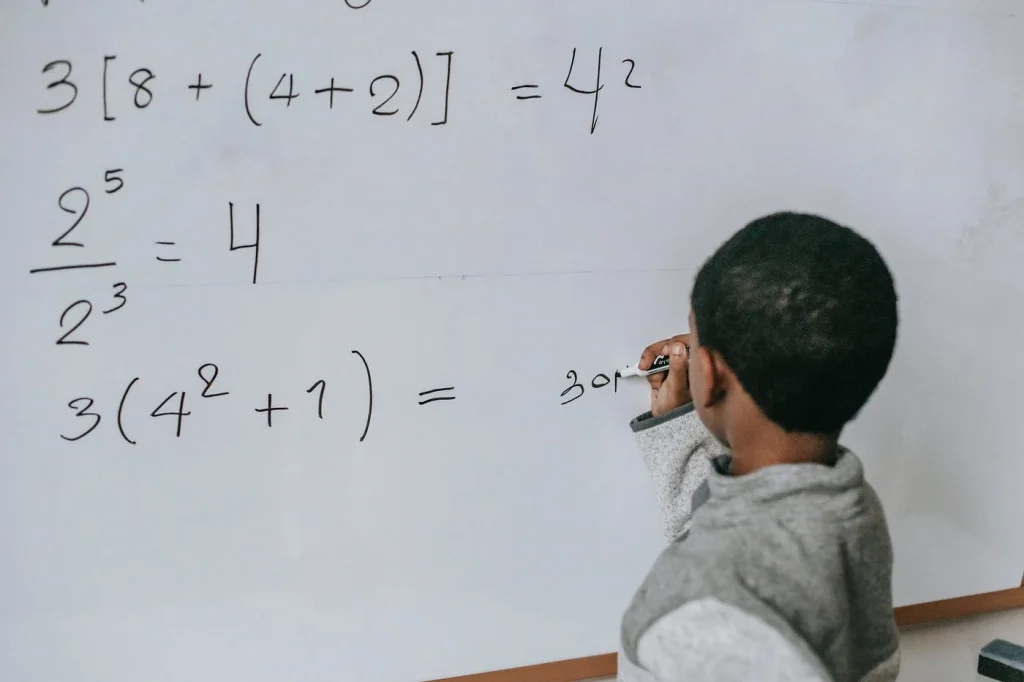
Strategies for Solving Problems
Effective problem-solving involves converting mathematical ideas into real-world situations. Encouraging learners to be critical and look at problems from different points of view improves their mathematical development.
Problem-solving promotes resilience and inventiveness in addressing mathematical challenges (source).
Effective Problem Solving Approaches
| Teach various ways of solving problems to students (e.g., guess and check, draw a picture, work backwards). |
| Give chances for unstructured problem solving tasks. |
| Highlight the importance of perseverance in tackling intricate issues. |
Communication through Mathematics Discussions
Engaging learners in mathematics discussions leads to better comprehension of ideas. Pupils articulate their reasoning by means of peer collaboration and classroom discourse that also enable learning from diverse perspectives.
Discussion-based learning enhances mathematical sense since it reinforces conceptual understanding and logical thinking (source).
How to Encourage Mathematical Discussions
| Pose open-ended questions that have multiple solutions. |
| Use Socratic questioning to guide discussions towards deeper understanding. |
| Create an environment where students feel free to share their math similar experiences with others. |

Real-World Applications
Bridging real-life scenarios and mathematical concepts enables learning that is meaningful and relevant to the students. By investigating how mathematics is used in various areas such as Finance, Engineering or even Art, learners get a wider perspective on its applicability and importance.
Proof of practical implication strengthens mathematical sense in terms of everyday use (source).
Examples of Real-Life Mathematics Applications
| Compute budgeting and financial planning. |
| Study data trends from scientific investigations. |
| Develop structures based on geometric principles. |
Use of Technology
Mathematical sense can be improved by technology that provides interactive simulations, virtual manipulatives, and adaptive learning platforms.
Digital tools allow for active learning experiences that support diverse learning styles of students. Inclusion of technology promotes exploration and fluency in mathematics (source).
Recommended Digital Tools for Enhancing Mathematical Sense
| Khan Academy, offering customized math tutorials. |
| Desmos for interactive graphing activities and geometry. |
| Mathletics for dynamic practice sessions and contests. |

Assessment and Evaluation for Learning
Assessment on a regular basis is critical to instructing as well as helping teachers track students’ growth in mathematics. Formative assessments such as quizzes, problem solving tasks, peer evaluations can provide valuable feedback concerning student understanding and identify areas that need reinforcement.
By monitoring the progress of the learner, the mathematical sense can be developed in an ongoing way (source).
Effective Strategies for Formative Assessment
| Pre-tests and post-tests should be implemented to assess learning outcomes. |
| Rubrics and scoring guides could be used for consistency during assessment. |
| Timely feedback that encourages reflection and goal-setting should be provided. |
Cross-Curricular Connections
Linking to other subjects gives math relevance in interdisciplinary learning. Students gain a comprehensive perspective on how mathematics fits within different disciplines by examining how it relates to science, art or social studies among others.
Cross-curricular connections widen mathematical sense (source).
Examples of Cross-Curricular Activities
| Data analysis in scientific investigations/ experiments. |
| The exploration of geometric shapes in art and architecture. |
| Historical trends; statistics from social studies study cases. |
Conclusion
It is crucial to nurture a sense of mathematics in learners so as to enable them become confident and capable problem solvers. By applying these 7 tactics- developing number sense, fostering problem-solving skills, using formative assessment practices and building cross-curricular relationships- teachers and students can enhance mathematical learning experiences.
These strategies improve number sense and promote critical thinking abilities and deeper understanding of the subject matter.
FAQs
What is mathematical sense?
Mathematical Sense refers to an intuitive grasp of or ability to make meaningful use of numbers, patterns or logical relationships. It includes recognizing math concepts when they appear in everyday situations and solving problems by applying logic.
Why is developing mathematical sense important?
Developing mathematical sense matters because it enhances critical thinking skills, problem-solving abilities, informed decision-making capacity in everyday life as well as academic achievements. It also provides a good foundation for success in school while opening up various career paths.
What can I do to develop my mathematical sense?
To develop a sense of mathematics in you, it is necessary to constantly solve problems, create logical tasks and puzzles, explore applications of math in life, take courses on this subject and ask for help if necessary. It is also crucial to develop a positive attitude towards studying math.
How does mathematical sense apply to everyday life?
In everyday life we can use mathematical sense when we need to manage our money, find out the price or compare prices while shopping, plan our trips and journeys, read data and statistics in newspapers as well as make practical decisions.
How can parents and educators contribute to children’s development of mathematical sense?
Encouragement of children’s positive attitude about mathematics; provision of many opportunities for experiences with hands-on mathematics activities; using games and activities that promote logical thinking; support for homework/learning resources; showing connections between math concepts.

Russell F. Jones, holding a Master in psychology from the University of Florida. He writes for Smart Parent Solutions, offering practical advice on parenting and child development. His engaging content helps parents navigate family life with confidence and ease. Russell enjoys sharing his knowledge and spending quality time with his family.
